Gravity
INTRODUCTION
- Last Updated On:
Introduction
We showed on the last page that an object moving under an inverse square force…
…moves in the polar equation:
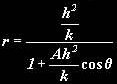
r is the distance from the centre of the force, θ is the angle between the object, the centre and the (arbitrary) axis, A is an arbitrary constant and h is a constant such that:
That is that at any point in its motion, it’s angular speed times the distance from the centre is constant. This formula is remarkably similar to that of the general polar equation of a conic:
Thus the objects path is a conic with the central object (e.g the sun) as its focus, where:
(Interesting fact: Focus is the latin word for ‘fireplace’. In his study of conics and orbits, Kepler realised that the sun was at one focus of the conic, hence, he called it fireplace.)
CONICS
Conics is the name given to a set of functions, because all of them can be acheived from cutting up a cone. They are a circle (cutting horizontally) an ellipse (cutting at an angle, but an angle less that the slope of the cone) a parabola (cutting parallel to the slope) and a hyperbola (cutting vertically).
Remarkably, all of these shapes have the same polar equation. Defining a point as the focus, the distance r from the focus of a point on the line at an angle Θ with the axis is
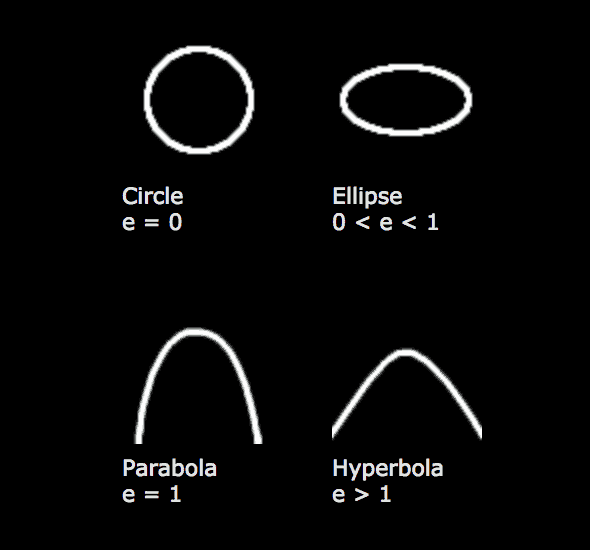
l is just a scaler, determining the size of the shape, the type of shape is determined by e, the eccentricty of the shape. Here are the four conics and the ranges of values of e which produce them:
GRAVITY
Now to apply these last two sections to gravity. We know that the force of gravity is given by:
Comparing this to our general formula, we can see that G M = k
We found that the centre of the force was the focus of the conic- if we are equating this to gravity, the sun is at the focus of a planet’s orbit. This proves Kepler’s first law.
What is h in the specific case of gravity? Remember that h is the constant equal to the angular speed of the object times its distance from the centre. Taking the point nearest the object, where its velocity is wholly transverse:
Where r0 is the closest the object comes to the centre (θ = 0) and v0 is the speed at that point, it’s initial speed if you like.
Its also worth noting at this point that we have just proved another one of keplers laws, that planets ‘sweep out’ equal areas in equal times. It can be shown by considering a small time Δt and calculating the area of the resulting ‘triangle’ that since r Θ (dot)is constant, the area it covers in a given time is constant, since it must travel faster when r is small and slower when r is large.
So how do we find e? Substituting A h2 / k for e in the inverse square path, and setting Θ = 0 and hence r0 = 0:
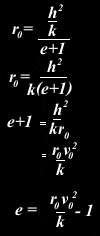
We said earlier that k is G M in the case of gravity (that is the mass of the cetral object times the universal gravitational constant). Remember that e determines the type of conic produced- we now have e in terms of real-life varaibles such as “initial” distance (closest approach) r0, “initial” speed (speed at closest approach) v0, the universal gravitational constant G and the mass of the central object, M. We can now tell whether an object will orbit, and what shape orbit it will have.
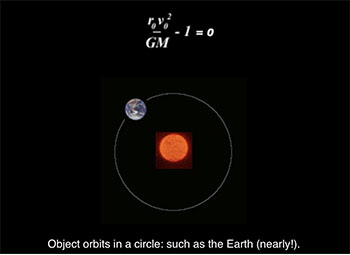
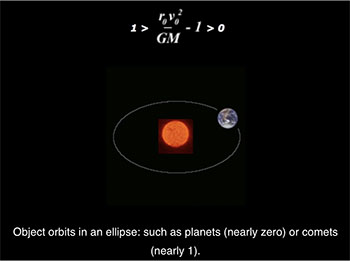
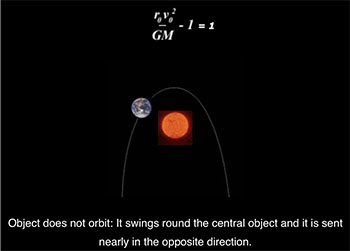
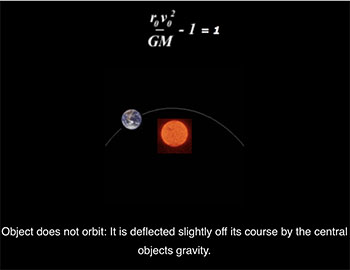
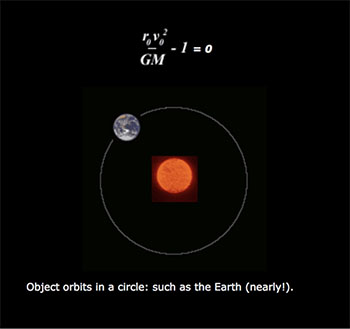
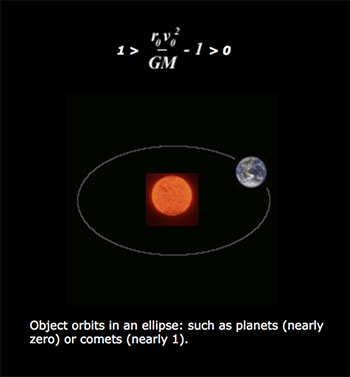

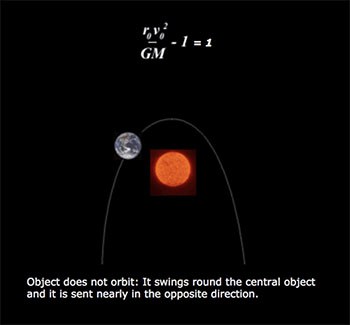
Amazing isn’t it- the elegance of it that something so complicated should reduce to neat little constant which determines whether and how orbits, and that such theoretical mathematics applies s perfectly in the real world. Funny as well, that the secrets to something so vast as the solar system and even the universe lay hidden in the humble cone.
Of course you can substitute in the other variables to get the equation fully in terms of real-life things, here it is if you want.
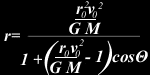
Its also possible from this to calculate the time period of the orbit. This ties in perfectly with Kepler’s laws, as it produces something of the form T2 = w a3, (where a is the distance from r0 to the centre of the ellipse, not the focus). Newton showed that the actual value of w, the constant is:
There you go- all three of Keplers laws are proved by this method:
- A planet’s orbit is an elipse with the sun at its focus.
- A planet’s orbit sweeps out equal areas in equal times.
- The square of semi-major axis (a) of a planets orbit is proportional to the cube of it’s orbital time period.
We’ve shown that these are true if the object in orbit is under a centripedal, inverse-square, attractive force, which we call gravity.
This is how my orbit simulator works- you can type in the variables (r0 and v0), and see if you can get the satellite orbiting the Earth in a circle. In thoery it should be an exactly scaled down model, with seveal million miles per pixel and so many months per second, using the equations above and the correct values of G and M (the mass of the Earth). Sorry but it only seems to work in Internet Explorer and Opera, but you can try other browsers (doen’t work in Mozilla Firefox, but let me know if it works in any others).
SUBSCRIBE TO OUR WEEKLY NEWSLETTER

