Gravity: AN INVERSE SQUARE LAW AND CONICS
PROOF THAT AN INVERSE SQUARE FORCE LEADS TO A CONIC
- Last Updated On:
AN INVERSE SQUARE LAW AND CONICS
Imagine an object moving subject to a force which constantly attracts it toward a fixed point. The magnitude of that force is in inverse proportion to the square of the distance between them, r (yes everyone, you can guess what I’m talking about!). How does the object move?
Mathematically the force is expressed:
Ther with the caret is the radial unit vector, signifying that this force acts wholly in the radial direction. To find the equation of the object’s path, we resolve forces in the radial direction using F=ma. Fortunately the only force is wholly in the radial direction. I don’t want to prove it, but for problems involving resolving radially, radial acceleration is given by:
So since F=ma we can write:
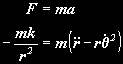
EQUATION 1
Since the only force is radial, there is no transverse acceleration. Again I don’t want to prove it, but when you resolve in the radial and transverse directions in problems such as this, it can be shown that transverse acceleration can be written as:
In this case, the transverse acceleration is zero, since there is no transverse force. So the rate of change of r2θ (dot) is zero, implying that r2θ (dot) must be constant. Let’s call it h:
Our goal is to eliminate time from equation 1, so as to get an equation involving r and θ, which will be the polar equation of the object’s path. It is useful (trust me!) to make a substitution at this point into the previous equation:
EQUATION 2
These will be useful later on. If we differentiate the substitution itself using the chain rule (both r and u vary with time remember) we can get expressions for the rate of change of r (radial speed), and the rate of change of rate of change of r (radial acceleration), which we can substitute in equation 1 and eliminate time. So, using the chain rule:
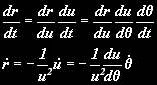
Since…
…from equation 2. We can make a useful substitution:
Differentiating again and making the same substitution:
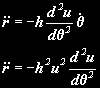
Now we can put all this stuff back into equation 1 and eliminate time!
Tidying up and making a few substitutions we get:
This is a second order differential equation, in u and θ. It can be solved using the standard method of solving second order equations. (You can skip this if you can just accept the solution to the equation, but I thought I’d include it for completeness)
THE AUXILIARY EQUATION
This has no real roots- it has complex roots of 0±j
THE COMPLIMENTARY FUNCTION
The roots are complex so the complementary function is:
Where α and β are the real and imaginary parts of the roots respectively, and A and B are arbitrary constants. Putting in α and β (0 and 1):
THE PARTICULAR INTEGRAL
The original equation is non-homogenous, (it doesn’t equal 0, there’s an extra constant- k/h2) so we need a particular integral of the form u=c (constant, as RHS is constant). Substituting into the original equation we find that c=k/h2
The General Solution is:
ACosθ + Bsinθ can be combined into a single a cos(θ + α) (because A and B are arbitrary constants its not necessary to work out the exact values of the new arbitrary constants in terms of them: we simply invent some new constants. So the general solution can also be written as (substituting u back for 1/r):
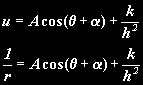
Since the α is just shifting the cos function, we can choose the x-axis so that α=0, making our equation:
Give yourself a pat on the back- you made it! Here we have the path in polar form of an object moving under an inverse square force.
Its not easy to see what shape this is so lets poke it around and see what happens…
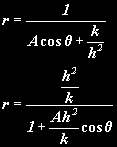
This looks very similar to the general equation of a conic (conics will be explained in greater detail on the next page).
THE GENERAL POLAR EQUATION OF A CONIC
In fact, it is a conic, where:
Wasn’t that fun? You may have guessed I didn’t choose an inverse square force at random. Lets have a look now at how all this relates to gravity.
SUBSCRIBE TO OUR WEEKLY NEWSLETTER

