The Solar System (Part 1)
HOW DO THEY KNOW THAT?
- Last Updated On:
Introduction
You’ve probably seen in books and magazines facts and figures they give for different things, like “Sirius is 8.7 light years away…” and “Each second the sun lets out enough energy to…”. If you’re anything like me you’ll wonder: how on Earth do they know that?
Always take claims with a pinch of salt- an astronomer’s viewpoint is limited to one point in time and space in the universe, hence, we can’t really be sure of anything. For instance I find it difficult to accept that we know exactly what happened 0.000000000001 seconds after the ‘big bang’, when we know only that the age of the universe is somewhere between 10 and 20 billion years old.
However, being so limited makes deducing information about the universe a challenge, and the ingenuity of some of the methods fascinates me.
Table of Content
RADIUS OF THE EARTH
The Greek mathematician and astronomer Eratosthenes calculated this in 200 B.C..
He knew that on a particular day in Syene, the sun would be directly overhead.
He set up a stick in Alexandria 5,000 stadia away (800-900 kilometres) on this day, and measured the angle of the shadow that the sun formed at midday.
He measured this to be 7.2°. He deduced that this is the same angle from the Earth’s centre that the distance between the two cities represents.
Since there are 360° in a circle, he worked out that 5,000 stadia is one-fiftieth of the circumference of the Earth. He therefore suggested the value of 250,000 stadia (40,000-46,000km).
Astronomers recently measured it using satellite equipment and submitted the figure of 40,008 km. From this, using the geometry of circles, he could calculate the Earth’s radius:
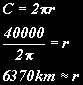
Pretty good for a man who lived 2,200 years ago who only used only a stick!

DISTANCE TO THE MOON
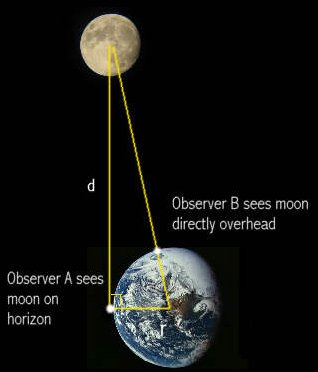
The distance to the moon can be determined by considering a very large imaginary triangle, and was first put forward by the Greek Hipparchus about 100 years after Eratosthenes suggested the radius of the Earth.
The moon is known to be directly overhead in one place, so if the place can be found where the moon is on the horizon at this time and the distance measured, it gives us the base for a very long, thin triangle (see diagram). The angle at A is a right angle, so:
Where θ is the angle at the Earth’s centre, which can be calculated by:
Where a is the measured arc length. Using this method Hipparchus estimated the distance to the moon to be 59 times the radius of the Earth (397,000km), which is not far off the modern accepted figure (382,000km).
This could likewise be repeated for all the planets, so that the distance from the sun for all the planets was known in terms of the distance from the Earth to the Sun (the AU):
| Planet | Distance from the sun |
|---|---|
| Mercury | 0.38 AU |
| Venus | 0.723 AU |
| Earth | 1.000 AU |
| Mars | 1.524 AU |
| Jupiter | 5.204 AU |
| Saturn | 9.582 AU |
HOW FAR AWAY IS THE SUN?
HOW FAR ARE THE PLANETS FROM THE SUN?
The first simple and very important question is actually quite difficult to answer, and an accurate figure eluded science until the seventeenth century. The same method as for the moon was tried, but failed due to the massive distance involved. To find the answer to the first question, we have to go the long way round and address the latter question first.
Johannes Kepler studied the orbits of the planets and found that the time period of a planet’s orbit squared in years is equal to the distance from the sun cubed in AU (that is, astronomical units, or the distance from the Earth to the sun):
So Earth has an orbital period of one year, so is 1 AU from the sun. Mars has an orbital period of 1.88 years (these orbital periods had been known since ancient times by observation) and so it’s distance from the sun is:
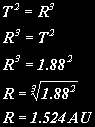
This could likewise be repeated for all the planets, so that the distance from the sun for all the planets was known in terms of the distance from the Earth to the Sun (the AU):
| Planet | Distance from the sun |
|---|---|
| Mercury | 0.38 AU |
| Venus | 0.723 AU |
| Earth | 1.000 AU |
| Mars | 1.524 AU |
| Jupiter | 5.204 AU |
| Saturn | 9.582 AU |
Astronomers only had to work out the actual distance to just one planet to find the distances to all the rest, including the Earth. This was achieved in 1672 when Giovanni Cassini measured the distance to Mars using Parallax.
This is a similar method to the one for finding the distance to the moon, forming a tall thin triangle.
The situation is more complex than the measurement of the distance to the moon however, as the two observers couldn’t be on opposite sides of the world because they wouldn’t both be able to see Mars at the same time and the triangle isn’t necessarily a neat right-angled or isosceles triangle, but the principle is the same. (Click here if you want to see the mathematics in more detail)
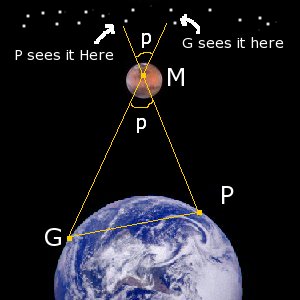
Cassini sent a colleague to French Guiana while he remained in Paris. At an agreed time the two measured the position of Mars against background stars (assumed to be at an infinite distance). When they met back again, they compared the two positions and measured the tiny angle of parallax.
Knowing this, and the distance (through the Earth) between the two locations (which can be calculated as the radius of the Earth is known), they could form a large triangle and calculate the length of one of the sides (which gives the distance between Mars and Paris).
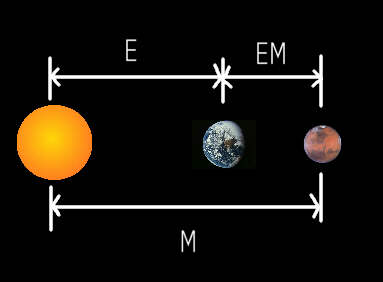
The figure they obtained was 93% accurate compared with the modern figure (78,000,000 km minimum between Mars and Earth).
The night they chose to do this was when Mars was at opposition to Earth, i.e. it was near enough exactly on the other side from the sun, giving the positions shown on the diagram on the left.
The distance that they measured, EM on the diagram, is clearly equal to M-E.
Since earlier we worked out that M=1.524 E from Kepler’s laws, we can use simultaneous equations to get E, the distance from the Earth to the sun in kilometers:
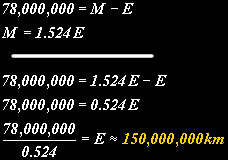
This is an extremely important result as it means that we can now work out the geography of the entire solar system, as we now know that 1 AU = 150,000,000 km
| Planet | Distance from the sun |
|---|---|
| Mercury | 58,000,000 km |
| Venus | 108,000,000 km |
| Earth | 150,000,000 km |
| Mars | 228,000,000 km |
| Jupiter | 779,000,000 km |
| Saturn | 1,433,000,000 km |
(When planets were discovered later their distances were calculated likewise). More accurate estimates of the AU were made in 1771 using the same method on Venus during a transit (when it passes in front of the sun).
Nowadays we can use this method but instead of measuring the distance to Venus with parallax, we can measure it directly and extremely accurately with radar.
A beam of radiation is aimed at the planet and the time it takes to receive the echo is measured using an atomic clock. Because the speed of light is known exactly the distance to Venus is half the time (the signal travels there and back) divided by the speed of light.
HOW HEAVY IS THE SUN?
A few years after Kepler died, Isaac Newton was born. In 1687 he published Philosophae Naturalis Principia Mathematica which was one of most influential books in physics.
In it he published his theory of gravity. His contemporaries suspected that Kepler’s laws could be a result of a centre-seeking force inversely proportional to the object’s distance, but no-one could prove it. Isaac Newton presented the correct mathematical proof that this was the case, and, that it was also proportional to the two masses involved (If you’re mathematically-minded I’ve written out such a proof- that an inverse square force produces elliptical orbits amongst others- on the gravity pages). This lead to Newton’s Universal Law of Gravitation:
Where G is a constant known as the Universal Gravitational Constant, which we will learn more about later.
We can now apply this to work out the masses of celestial objects. If we assume that the planet moves in a circle (which is a good assumption for many orbits… the same calculation can be applied to eliptical orbits- the mathematics just becomes a bit more complex when you allow for eccentricity) then there is a constant, centre-seeking (centripetal) force. For any object moving in a circle it is known that the centripetal force acting on it is given by:
Where m is the mass of the object, r is the radius of it’s motion and T the time for 1 full revolution. In our case of objects in orbit, this centripetal force is gravity, so we can equate the two forces:
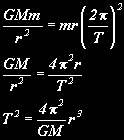
Notice the similarity between this and Kepler’s law above. This was the proof of Kepler’s third law. Now we have a formula relating time of orbit, distance from sun (in real measurements, not AU), and mass. Rearranging the formula to make mass the subject gives:
So we can find an object’s mass if we know the time period of and distance to an orbiting object.
But how do we know what the value of ‘G’ is? That is a very good question, to which Newton did not really know the answer. It was not until 1798 that a reliable figure was established by an experiment conducted by Henry Cavendish. He set up two masses on either end of a rod hung by a string, free to turn. He moved two very large masses near the two smaller masses and measured the twist in the string that this produced (for more detail about the experiment see this page by the Physics Classroom). His experiment resulted in a value of 6.75×10-11 for G, which is not far from it’s modern value, 6.67×10-11. This is an extremely small number, which explains why we only appreciate gravitational force when it comes to very large masses.
We are now free to calculate the mass of any object which has a satellite (if we know it’s period and distance) This includes the Sun (by looking at any of the planets) Earth (by looking at the moon) or Jupiter (by looking at it’s moons).
The Earth has a period of 365.24x24x60x60 seconds (31,556,296 seconds) and orbits at a distance of about 150,000,000 km (150,000,000,000 metres) so the mass of the sun is:
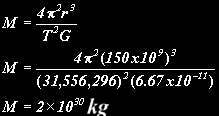
HOW HEAVY IS THE EARTH?
The Moon has a period of 2,551,443 seconds and orbits at a distance of about 384,403,000 metres (its orbit may be assumed to be roughly cicrular) so the mass of the Earth is:
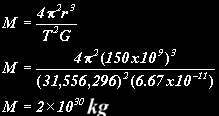
However, there is a more accurate way to determine the Earth’s mass that doesn’t depend on the accuracy of our knowledge of the distance to the moon.
An object’s weight on Earth is equal to the Earths gravitational pull on it, using Newton’s second law that F=ma (force = mass x acceleration):
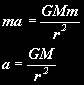
However, there is a more accurate way to determine the Earth’s mass that doesn’t depend on the accuracy of our knowledge of the distance to the moon.
An object’s weight on Earth is equal to the Earths gravitational pull on it, using Newton’s second law that F=ma (force = mass x acceleration):
The value of g can be accurately be determined by experiment to be 9.8ms-1. Rearranging then, to get M, the Mass of the Earth is:
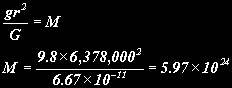
HOW HEAVY IS JUPITER?
A similar method can be applied to find the mass of Jupiter, Saturn, or any planet with an observable moon.
First, though, we need to find out how to work out an object’s size from observation, if we know how far away it is.
Things look bigger close up than they do further away. This obvious truth is because an further object has a smaller angular diameter than a close one (see diagram).
We can measure directly an objects angular diameter from where we are, so if we know how far away it is we can work out how big it is. The actual size of an object is calculated by:
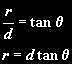

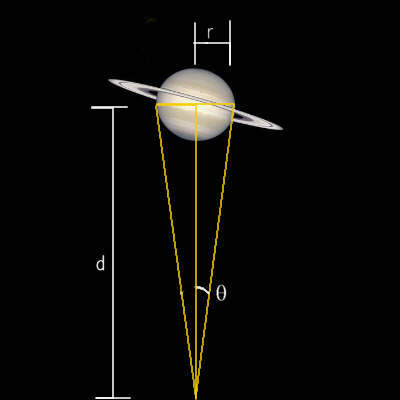
Where θ is the object’s angular radius, d is the distance to the object, and sis the actual radius of the object (see diagram on the right). You could think of it as parallax in reverse- the triangle is upside down.
Now, we know how far away Jupiter is, so by measuring the angular size of the radius of the orbit of Jupiter’s moons, we can work out it’s actual radius by using the method above. Let’s look at one of Jupiter’s four large moons, Io. We can calculate the radius of it’s orbit to be 421,600 km using this method. We observe it to take 152,841 seconds to orbit the planet. Using the same calculation for the mass of the sun, then, we can calculate Jupiter’s mass:

Note that the principle that you can find the size of an object if you know how far away it is applies to anything; whether it be objects here on Earth, the Moon, the Sun, Neptune, The Orion Nebula, or even whole Galaxies.
It can even be used to find the size of craters on the moon, mountains on Mars or the size of Jupiter’s great red spot. Bear in mind as well that now you know the size and mass of objects, you can easily calculate their volume and average density.
HAVE A GO YOURSELF
Try this question (you’ll need a calculator, and maybe a piece of paper and pen)
When Saturn is at opposition to Earth (when the Sun, Earth, and Saturn are in a line) the radius of orbit of Titan, one of Saturn’s moons, is measured. It has an angular size of 194 arcseconds (that’s 194/3600ths of a degree)
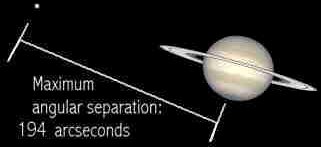
It’s time period is observed to be 1,377,648 seconds. You know that Saturn is 1,443,500,000,000m from the sun and Earth is 149,600,000,000m from the sun (Gis 6.67×10-11). What is the mass of Saturn?
All the methods needed are listed above. Think- what do you need to know to work out an central objects mass?
- Work out the distance from Earth to Saturn- remember the Sun, Earth and Saturn are all in a straight line.
- Work out the actual radius of Titans orbit. You know how far away it is and it’s angular radius, so you can work out its actual radius.
- You now know the radius and time period of an object orbiting Saturn, so use Newton’s law of gravitation to work out Saturn’s mass.
To find Saturn’s mass we need the time period and radius of an object orbiting it.
To find the radius of orbit we need to know how far away it is.
The Sun, Saturn and the Earth are in a straight line, so the distance from Earth to Saturn is the distance from the sun to Saturn take away the distance from Earth to the Sun:
![]()
Titan’s orbit has an angular radius of 194 arcseconds, so now we know its distance we can calculate its real radius of orbit:
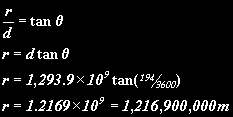
Now we know Titan’s orbital radius and time period, we can calculate the mass of Saturn:
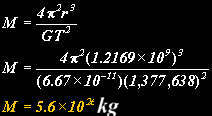
SUBSCRIBE TO OUR WEEKLY NEWSLETTER

