Distance to Mars
ASTRONOMY
- Last Updated On:
Lets call the observer in Paris P and the observer in Guiana G. First We need to calculate the x, y and z co-ordinates of the two locations (relative to the centre of the Earth), We can do this using latitude and longitude:
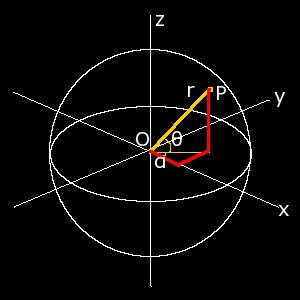
Where latitude = θ and longitude = α and r is the radius of the Earth. The x, y, z components of OP (yellow) are marked in red. Study of the diagram using trigonometry tells us that:
x = r cos θ cos α
y = r cos θ sin α
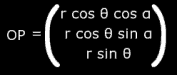
The x, y and z components of OG can be calculated likewise. We can now find PG as a vector by OG – OP
We can calculate the length of the resulting vector using 3-d Pythagoras rule, squaring the x y and z components, adding them up then square-rooting it. Dividing the vector by this number gives us a unit vector, that is a vector which has the same direction but length 1.
Next we need to find the vector PM:
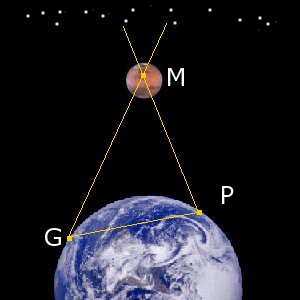
We can measure the celestial “Latitude and Longitude” (Declination and Right Ascension) as it appears from P, hence we can calculate its x y and z components in terms of its distance. Clearly we don’t know distance at the moment (that’s what we’re trying to work out), but as we’re only trying to find the direction of PM (getting a unit vector) we can assume that r = 1. Putting this into the equation above gives us a our vector for PM.
Now we can calculate the angle GPM using the scalar (dot) product:
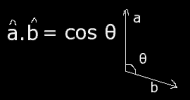
Where a and b are the two unit vectors (PG and PM) and θ is the angle between them. (To actually calculate the dot product of two vectors you sum the products of each component).
Angle PMG is the angle that is measured in the experiment, when the two observers meet and compare the apparent position of Mars against the background stars. So now we now know two angles in our triangle, therefore we can work out the third (180° – the other two).
Since we know at least two angles and one side, we can now calculate the lengths of the other sides, in particular the length of PM, the distance from Paris to Mars (which is approximately equal to the distance from the centre of the Earth to Mars), using the sine rule:

Where in our case a is the distance |PM|, angle A is the angle PGM (which we calculated from 180° – the other two), angle B is the measured angle of parallax and the length b the distance between the two observing locations, which we calculated at the beginning.
This provides us with our figure for the approximate distance between Earth and Mars (indeed any object close enough to have a measurable angle of parallax). The figure obtained in 1672-73 was about 7% out, which is understandable given the sources of error in the experiment- the tiny angle involved, exact longitudes not being known, error in the figure for the radius of the Earth, and errors in timing (without instantanious communication).
SUBSCRIBE TO OUR WEEKLY NEWSLETTER

