THE CELESTIAL SPHERE
- Last Updated On:
Introduction
As people first started to map out the night sky, it became necessary to have a standard, universal way of plotting positions of objects in the sky. As the stars appear to occupy fixed positions in the sky relative to each other, a convenient way of thinking about the situation would be to imagine the Earth placed at the centre of a larger sphere.
The stars occupy fixed positions on the surface of this ‘celestial sphere’, and the Earth rotates within it. This is obviously not the case in real life but it is a good model because this is pretty much how things look from our point of view.
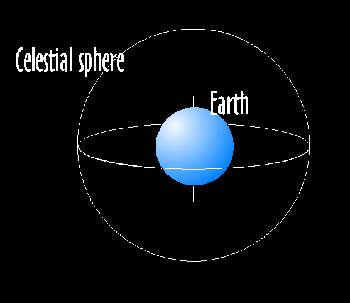
The Earth rotates within this sphere, but of course, to us it appears as though the celestial sphere is rotating, on the same axis as the Earth. If the line of the Earth’s axis were extended to infinity, the point where it meets the celestial sphere is called the celestial pole.
If we take the Earth as fixed, all the stars appear to rotate around this point. In the Northern Hemisphere, we are fortunate to have a star more or less exactly on the celestial pole, Polaris. If you go out on a clear night and look at a certain constellation several times over a period of hours you will notice it appears to rotate around the celestial pole.

The same applies to all latitudes, if our observer at 45° latitude looked straight up, he would be looking at a point on the 45° line of declination.
I live on 51° latitude, so the line of 51° declination passes directly overhead from my position.
Generalising this, the angle between the celestial equator and the zenith, (that is, the declination) anywhere on Earth is equal to the latitude at that point. This leads us to some useful results:
THE DECLINATION
Now imagine the Earth’s Equator extended out to infinity, the corresponding point on the celestial sphere is the celestial equator. Just as the angle between the pole and the equator on Earth is a right angle, the same is true of the celestial sphere. For this reason points on the celestial equator are said to have a declination of 0° and the celestial pole is said to have a declination of 90°.
Note that declination is analogous to latitude on Earth, where the pole has a latitude of 90° and the equator has a latitude of 0°. Of course, we can also imagine lines in between of declination 10°, 20°, 30° etc., corresponding to latitude on Earth, and note also that lines South of the equator have negative declinations (e.g. -76° is 76° South).

Parts of a degree are measured in arcminutes (60 arcminutes per degree) and seconds (60 arcseconds per arcminute). So you may see a particular declination given as -7° 27′ 03″, which means 7 degrees 27 minutes and 3 seconds South, which is just under 7 and a half degrees South of the celestial equator.
In reality arcseconds are much too tiny for us to worry about, rounding to the nearest half-degree is usually more than accurate enough.
The relationship between declination and latitude does have a real significance, as it enabled sailors for thousands of years to find out their latitude, but I’ll come on to that later.
RIGHT ASCENSION
Obviously we can’t set points with only one coordinate, another set is needed, just as longitude was needed on Earth to be able to define a point completely. Right Ascension (RA) is the celestial equivalent of longitude. Just as longitude doesn’t have so much of a natural significance, so was arbitrarily centred on Greenwich Observatory, London, RA was defined to be zero at the first point in Aries.
Because the Earth is turning the stars appear to turn- but since there there is no movement North-South lines of declination stay fixed- this is why they are more significant.
As the stars appear to rotate East-West, lines of RA move- they complete one full turn per day (well, actually a little bit more due to the fact the Earth has moved about 1° round the sun in a day, but this is small enough to be ignored day-to-day).
This means that a particular star moves through 15° per hour.

So, it is convenient for us to measure Right Ascension in hours, where 15 degrees is an hour and 360 degrees is 24 hours. This is further divided up into minutes and seconds (not to be confused with arcminutes and arc seconds, which are not the same thing) in the same way that time is divided, i.e. an hour is 60 minutes, a minute is 60 seconds etc.

If you were looking at a star through your telescope say at 50° declination and 0hrs RA, in 1 hours’ time you would be looking at 1hr RA, then 2 hours later at 2hrs RA and so forth. In fact, after say, 3 hours, 56 minutes and 12 seconds, you would be looking at 3hrs 56mins 12sec Right Ascension!
So now we have two co-ordinates, we can plot any point on the surface of the celestial sphere. For instance the Orion Nebula has co-ordinates -5° 27′ Dec, 5h 35m 24s. RA The Andromeda Galaxy has coordinates 41° 16′ Dec, 0h 42m 42s RA.Important to grasp is that although these objects appear to move, their co-ordinates are fixed because they stay the same relative to each other.
THE VIEW FROM HERE…
How does this look from where we are? Well, this depends on your position on the Earth.
THE VIEW FROM HERE…
How does this look from where we are? Well, this depends on your position on the Earth.
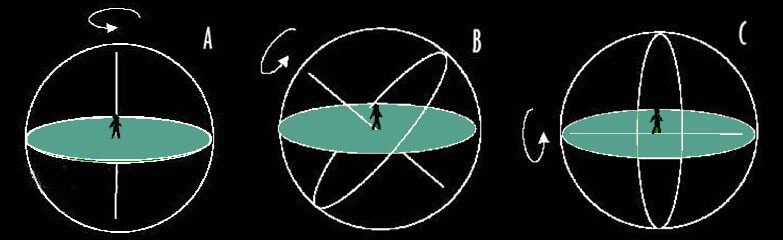
Observer A has the Celestial pole directly above him, being at the Earth’s pole. The stars simply rotate in a circle around our observer. The celestial equator is on the horizon- he can only see stars in the celestial Northern Hemisphere.
Observer C has the celestial equator directly above him, being at the Earth’s Equator. The celestial poles are at opposite ends of the horizon and the stars arc over head, directly East-West. From here is the only latitude you get to see all the stars because equal amounts of the Northern and Southern Hemisphere are visible, and as Earth turns all positions on the celestial sphere are visible at one point.
I came to Observer B last, because most of us are in his position. Our observer is at 45° latitude but this applies to anywhere between the two extremes of pole and equator. The observer at 90° latitude had 90° declination directly above him (at his zenith), and the observer at 0° latitude had 0° declination at his zenith.
The same applies to all latitudes, if our observer at 45° latitude looked straight up, he would be looking at a point on the 45° line of declination.
I live on 51° latitude, so the line of 51° declination passes directly overhead from my position.
Generalising this, the angle between the celestial equator and the zenith, (that is, the declination) anywhere on Earth is equal to the latitude at that point. This leads us to some useful results:
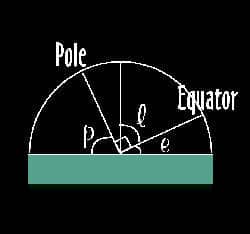
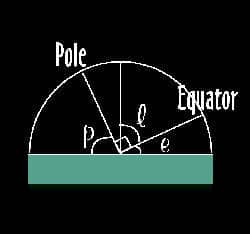
From geometry, it is easy to see that angle p, the elevation of the celestial pole from the horizon, is equal to angle l, the latitude. This is very important in navigation, as it allowed ancient sailors to tell their latitude by measuring the elevation of the celestial pole (in the Northern Hemisphere, this is easy because Polaris, a bright star lies near enough on the pole.)
So if you’re ever lost in the snaky swamps of some strange country, or get shipwrecked and you’re marooned on some desert island, you know how to find your latitude- the elevation of the celestial pole.
Note also that the celestial equator always intersects the horizon exactly at East and West, wherever you are. To find the celestial equator, find the pole first. Look 90° one way, then the other, these are East and West. Then turn round through 180° so you’re facing the opposite way. At this point (opposite the pole) the equator is at an elevation from the horizon of 90° – your latitude, and it runs from East, through this point, then down to meet the horizon again at West. It will help you if you learn where the celestial pole and equator are where you live. Now you can see how the stars appear to move: following the line of the celestial equator, rotating around the pole.
If you want to see a demonstration of this look at these time-lapse photographs taken from all over the world, showing the apparent motion of the stars. Note how the position of the celestial pole varies with latitude, e.g. on Mt Kilimanjaro 3° south the (south) pole is 3° above the horizon.
YEARLY MOTION
As I mentioned earlier, the stars daily rotation is just over a full circle, about 1° over- because the Earth has moved about 1° round the sun. This means that over the course of a year, the stars appear to complete one whole turn. If you went out and looked at a particular constellation over a period of months at the same time, it would appear to slowly move around the pole in the same direction as the daily motion- about 30° (or 2 hours of Right Ascension) a month. This also means that the constellations obscured by daylight slowly come round to be visible at night as the year progresses.
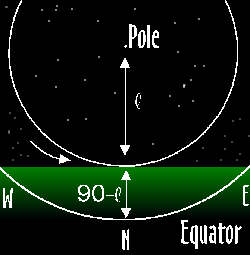
So do I get to see all the stars on the celestial sphere at some point? Well, not usually, unless you live exactly on the equator.
The pole is inclined at an angle equal to your latitude, so the equator is below the horizon at an angle of 90° – your latitude.
Stars above the declination of 90° – your latitude never set.
For instance, I live at 51° latitude, so the pole is at an elevation of 51°. Stars at 39° declination at their lowest point just touch the horizon, and all the stars at a declination above 39° never set:
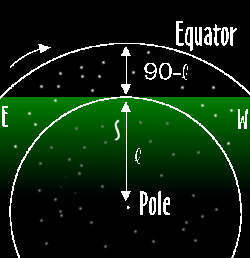
(Note the diagram is drawn illustrating the Northern Hemisphere, but it applies equally in the Southern Hemisphere, if you reverse the directions.) Angle l is your latitude. The stars inside the white line never set, either daily or yearly. Outside this line the stars rise and set at different times of the day and year. Conversely, looking opposite the pole:
The stars below the white line, those with a declination greater than 90° – your latitude below the equator at their highest point still are below the horizon, so they never rise, either daily or yearly.
This means you only ever see stars in your Hemisphere (declination greater than 0° in the Northern hemisphere and declination less than 0° in the Southern hemisphere), and the stars in the other hemisphere with a declination of 90° minus your latitude.
EQUATORIAL MOUNTS
Now you might understand the equatorial telescope mount better. It aligns the telescope with the Earth’s axis, so that instead of moving up and down and turning around (alt-az mount), it moves in the Declination direction and the Right Ascension direction. This means you only have to turn the RA axis to keep an object centred. It also means you can look up the celestial co-ordinates of an object, then set the telescope’s dials to the right values and you should be looking right at it.
To align an equatorial mounted telescope, first of all you need to make sure that it is set at an angle equal to 90° – your latitude facing the pole. You can use a compass to get the right direction in the Southern Hemisphere, in the Northern Hemisphere, just point it at the North star. It obviously involves a little more care than that, and not owning an equatorial telescope, I’m not really qualified to give an expert tutorial on it, however here are some links to pages to help you.
SUBSCRIBE TO OUR WEEKLY NEWSLETTER

